Введение. Земли лесного фонда занимают около 65% от общего количества земель в РФ, что составляет 1105 млн.га. К ним относят лесные (т.е. земли, покрытые лесной растительностью и не покрытые ею, но предназначенные для ее восстановления) и предназначенные для ведения лесного хозяйства нелесные земли [1]. Лесной фонд РФ находятся в федеральной собственности. В соответствии с федеральным законом допускается передача части лесного фонда в собственность субъектов РФ. Гражданский оборот, т.е. купля-продажа, залог и совершение других сделок, которые влекут за собой отчуждение участков лесного фонда, не допускаются. Участки лесного фонда предоставляются гражданам и юридическим лицам на следующих правах пользования: аренды, безвозмездного пользования, концессии и краткосрочного пользования [2]. Происходящие последнее время изменения климата, различные геологические изменения приводят к увеличившемуся числу лесных пожаров (не только на территории России, но и по всему миру). В следствие этого возникает вопрос адекватности проводимых работ, направленных на восстановление лесных ресурсов. Поэтому целью работы является не только анализ и моделирование процесса лесовосстановительных работ, но и выявление взаимосвязи между лесовосстановительными работами и пожарами, возникающими на территории лесных земель.

В качестве объекта исследования рассмотрим временной ряд лесовосстановительных работ на территории РФ за период с 1992 по 2015 года.

1. Анализ основной тенденции. Тест Фостера-Стюарта показал наличие тенденции в исследуемом ряду и, сравнивая линейную, параболическую, гиперболическую и показательную функции, в качестве уравнения основной тенденции была выбрана квадратичная регрессия:

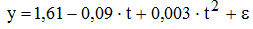   . Коэффициент детерминации данной модели составляет R²=0,886 и все параметры значимы по критериям Стьюдента и Фишера. Здесь параметр b₀ показывает начальные условия развития процесса, т.е. размер лесовосстановительных работ в 1992 г. составил 1,61 млн.га; параметр b₁ – скорость процесса, другими словами, с каждым годом лесовосстановительные работы уменьшаются на 0,09 млн.га; параметр b₂ – ускорение, т.е. изменение лесовосстановления растет каждый год на 0,003 млн.га.

Проведём анализ адекватности выбранных моделей с помощью исследования их ошибок на независимость, случайность и нормальность распределения:

— нормальность остатков может быть проверена с помощью показателей асимметрии и эксцесса [3]:

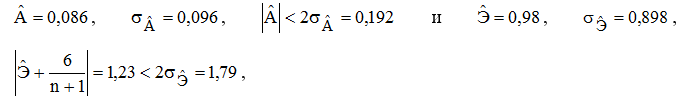
следовательно, остатки распределены нормально;

— независимость остатков можно проверить с помощью критерия Дарбина-Уотсена [4]: d_L =1,26 и d_U=1,44, тогда 4-d_U=2,56 и 4-d_L=2,74, фактическое значение d=1,47 принадлежит интервалу [d_U, 4-d_U], следовательно, гипотеза о независимости случайных отклонений принимается;

— случайность остатков можно проверить с помощью критерия медианных серий [5]: число серий v(24)=7, протяжённость самой длинной серии k_max(24)=3, тогда

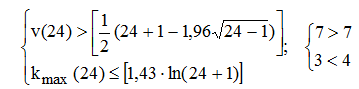и, следовательно, ряд остатков можно считать случайным.

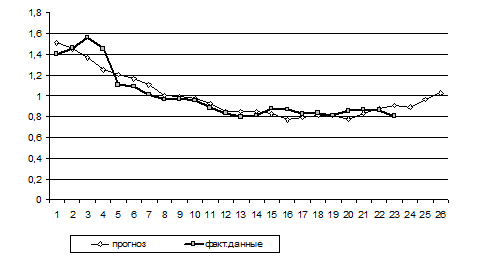
Рисунок 1. Исходные данные, прогноз и экстраполяция на 3 уровня

2. Анализ периодических колебаний. Анализ автокорреляционной функции показал, что изменение размера лесовосстановительных работ имеет цикличность с периодом τ=4. Для моделирования сезонных колебаний могут быть использованы модель с индексом сезонности и тренд-сезонная модель [6]. Построив обе модели и сравнив их ошибки аппроксимации, мы получили, что необходимо использовать аддитивную тренд-сезонную модель с квадратичным трендом. Скорректированные индексы сезонности для нашего ряда составили:

   

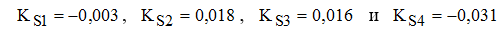
   а модель прогноза приняла вид:

   

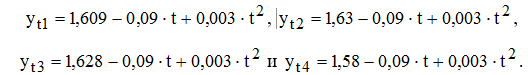
   Ошибка аппроксимации данной модели составляет 6,03%. Исходные данные, прогноз и экстраполяция на 3 уровня представлена на рис. 1.

Таким образом, исследование показало, что фактический размер лесовосстановительных работ имеет явную тенденцию к сокращению, однако теоретический прогноз обещает их рост. Во-вторых, лесовосстановительные работы имеют выраженный сезонный характер, а именно снижение каждый 4-й год относительно среднего уровня. На наш взгляд снижение может быть объяснено формированием бюджета страны на 4 года и прогнозные доходы государства имеют тенденцию к сокращению.

3. Анализ коинтеграционных связей. Переходя к изучению взаимосвязи с размером земель, пройденных пожарами, не ограничивая общности обозначим у₁ – лесовосстановление (млн.га), у₂ – лесные земли, пройденные пожарами (млн.га). Проверим гипотезу о наличии коинтеграции между рядами на основе критерия Ингла-Грэнджера. Строим линейную регрессию влияния сгоревших лесов на размер лесовосстановительных работ:

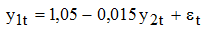   , параметр b₁ данного уравнения значим при α=5%, R²=0,719 и он значим по критерию Фишера. Определяя остатки по данной регрессии, строим зависимость вида: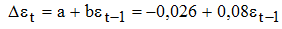. Расчетное значение t-статистики для параметра b равно 0,67; критическое значение критерия Ингла-Грэнджера при α=5% равно 1,9439 [7]. Таким образом, гипотеза об отсутствии коинтеграции между рядами принимается, т.е. с вероятностью 95% можно говорить об отсутствие динамики изучаемых временных рядов. Другими словами, лесовосстановительные работы никак не связаны с размером лесных земель, пройденных пожарами.

Коэффициент корреляции между рядами составляет r=-0,28. Коэффициент корреляции для рядов отклонений равен 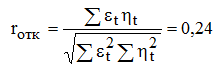,где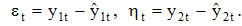

Данный показатель говорит об отсутствии ложной корреляции между рядами, т.е. действительно наблюдается слабая зависимость в размерах восстановленных и сгоревших лесов.

Для моделирования регрессионной зависимости между исследуемыми показателями воспользуемся уравнением регрессии по отклонениям от трендов [8]: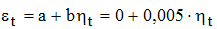. Коэффициент детерминации R²=0,19 и он значим по критерию Фишера. Коэффициент b значим и он говорит о том, что случайные отклонения по ряду у₁ – ряду лесовосстановительных работ –  в 0,005 раз выше случайных колебаний в ряду у₂ – ряду динамики сгоревших лесных земель.

Данное уравнение можно использовать для прогноза переменной у₁ в зависимости от предполагаемого изменения переменной у₂. Имеем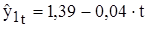,,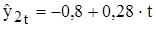 тогда.

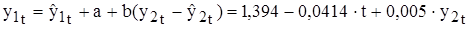Параметр b₁=-0,0414 говорит о том, что воздействие всех факторов, кроме размера земель, пройденных пожарами, на размер лесовосстановительных работ приведёт к его среднегодовому абсолютному снижению на 41400 га. Параметр b₂=0,005 показывает, что если размер сгоревших земель увеличится на 1 млн.га, размер лесовосстановительных работ увеличится лишь на 5000 га.

Результат. Составим прогноз размера лесовосстановительных работ на основе построенной модели:

— для 2016 год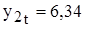а: , а 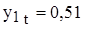, т.е. если размер земель, пройденных пожарами составит 6,34 млн.га, то размер лесовосстановительных работ – 0,51 млн.га;

— для 2017 год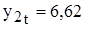а:, а;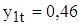

— для 2018 год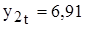а: , а.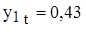

Таким образом, можно увидеть, что согласно полученной модели размер лесных пожаров будет только увеличиваться, а лесовосстановительные работы только сокращаться. Также исследование показало, что проводимые лесовосстановительные работы не зависят от размера земель, пройденных пожарами, что не согласуется с Лесным кодексом.