Применение теории портфельного инвестирования для решения задачи сельскохозяйственной диверсификации
Application of the Theory of Portfolio Investment to Problem of the Agricultural Diversification
Abstract: The article is devoted to application of portfolio analysis methods to solve problems related to the distribution of funds across different land endowment for growing crops. In the process of agricultural activity, the question of determining the share of participation in various farms often arises. If the net income from a farm is considered in probabilistic terms and it is assumed that the farmer is provided with a certain amount of land, the problem of choosing the optimal combination of farms can be interpreted as a special case of a problem of forming a securities portfolio. This article is directed to assess the applicability of the theory of portfolio analysis to the problem of agricultural diversification or, on the other hand, to study the conditions under which the only diversification strategy is implied for farmers who make decisions. Based on hypothetical data, an effective border of the feasible set of diversification strategies for two farms has been constructed. The possibility of application the separation theorem for agriculture has been considered and various options for the main objective of agricultural diversification have been analyzed.
Keywords: diversification, portfolio analysis, agriculture, farm, expected return, risk, standard deviation, effective border
Введение
Предположим, лица, занимающиеся сельским хозяйством (объединим их общим названием «фермеры»), сталкиваются с проблемой распределения средств по различным земельным участкам для выращивания сельскохозяйственных культур (т.е., по сути, определения доли участия в различных фермерских хозяйствах). Часть участков находится в собственности фермеров, часть предоставляется им в пользование (как правило, в аренду).
Задача отбора комбинаций участия в фермерских хозяйствах для фермера по своей природе похожа на задачу формирования портфеля для инвестора. То есть, когда чистый доход от фермерского хозяйства рассматривается в вероятностных терминах и предполагается, что фермер обеспечен определенным количеством земли, задача выбора оптимальной комбинации фермерских хозяйств может интерпретироваться как особый случай задачи формирования портфеля. Признание сходства этих двух задач обеспечивает основу для применения методов портфельного анализа для исследования диверсификации на примере фермерских хозяйств. В частности, теорема разделения и непосредственные выводы из нее определяют решение задачи фермерской диверсификации при условиях, до некоторой степени общих, касающихся и отношения лица, принимающего решение, к риску, и допустимого множества, определяемого альтернативным набором фермерских хозяйств. Когда земля рассматривается в качестве авансированного капитала, а рисковые фермерские хозяйства – в качестве ценных бумаг, результаты, связанные с теоремой разделения для портфельного анализа, могут быть применены к задаче сельскохозяйственной диверсификации.
Исследования в менеджменте сельского хозяйства и в производственной экономике можно проводить по образцу классической задачи формирования портфеля Г.Марковица (подробнее см., например, [6][7]). То есть, можно вычислять вероятностное распределение чистого дохода от фермерских хозяйств и определять пропорциональные комбинации фермерских хозяйств, которые минимизируют дисперсию альтернативных уровней ожидаемого чистого дохода (в терминах Г.Марковица — эффективного множества портфелей). Если предполагается, что фермеры, принимающие решения, несклонны к риску, этот анализ способствует решению задачи диверсификации путем введения ограничения соответствующих альтернатив в допустимом множестве стратегий. Данная статья направлена на оценку применимости теории портфельного анализа к задаче сельскохозяйственной диверсификации или, с другой стороны, на исследование условий, при которых для фермеров, принимающих решение, подразумевается единственная стратегия диверсификации.
Постановка задачи.
Пусть xi – доля участия в i-ом рискового фермерском хозяйстве, i = 1…N. Предполагается, что доли участия не могут принимать отрицательные значения, а также, что их сумма равна единице. Распределение чистой доходности Ri на единицу площади обрабатываемой земли (предположим, один гектар) от i-го рискового фермерского хозяйства характеризуется двумя параметрами: E(Ri), или – математическое ожидание доходности и – дисперсия. Количество однородной и делимой земли, которая предоставлена фермеру (земельный участок), обозначим S. Задача диверсификации, следовательно, состоит в том, чтобы найти оптимальную стратегию для комбинации долей участия в рисковых фермерских хозяйствах, а именно, вектор x = (x1, x2,…xN). Выбор этой диверсификационной стратегии зависит, в основном, от целевой функции фермера и от допустимого множества фермерских хозяйств в связи с особенностями фермерской ситуации.
Для определения целевой функции задачи предположим, что фермер, принимающий решение, рассматривает доход от любого фермерского хозяйства с вероятностной точки зрения. Т.е., фермер рассматривает чистую доходность, ассоциирующуюся с каждым из N фермерских хозяйств, как имеющую вероятностное распределение. Также предполагается, что в оценивании привлекательности альтернативных комбинаций фермерских хозяйств фермер желает действовать на основе двух параметров распределения – ожидаемой доходности и стандартного отклонения. Фермер имеет предпочтения, которые могут быть представлены функцией полезности (подробнее о функции полезности и предпосылках теории предпочтений см., например, [4]).
U = f(E, s)
Кривые безразличия, соответствующие этой функции полезности, представлены на рис.1.
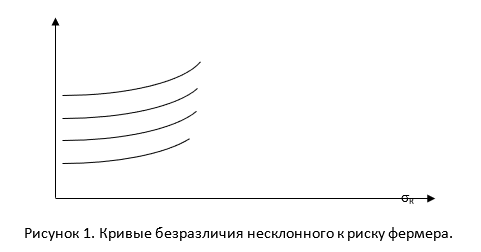
Ограничения могут задачи быть представлены в виде множества допустимых планов (фермерских хозяйств) аналогично множеству допустимых портфелей, жирная линия, ограничивающая допустимое множество, представляет собой эффективную границу (рис.2):
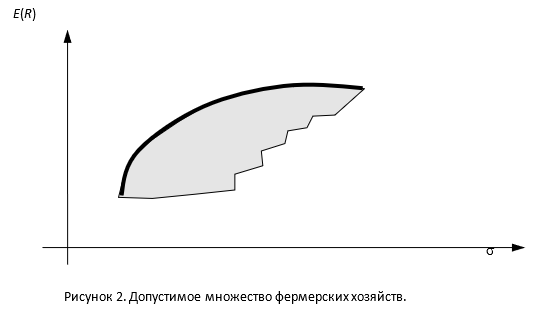
Покажем на условном примере, как выглядит эффективная граница для двух рисковых фермерских хозяйств. В качестве ожидаемой доходности будем использовать средневзвешенную доходность от выращивания сельскохозяйственных культур в фермерских хозяйствах (весами являются доли участия в хозяйстве), а дисперсию будем вычислять по формуле из классической теории портфеля ценных бумаг:
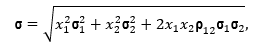
где r12 – коэффициент корреляции между доходностями двух фермерских хозяйств.
Предположим, имеются данные о доходностях и риске (стандартном отклонении) двух альтернативных вложений денежных средств: в обработку земли, отводимой под выращивание ржи, и в обработку земли, отводимой под выращивание пшеницы, – доходность первого фермерского хозяйства R1 = 10%, доходность второго R2 = 12%; s1 = 14%, s1 = 15%; r12 = 0,9. Рассмотрим 11 различных комбинаций участия в фермерских хозяйствах (табл.1).
Таблица 1
Доли участия в фермерских хозяйствах.
| x1 | x2 |
| 1 | 0 |
| 0,9 | 0,1 |
| 0,8 | 0,2 |
| 0,7 | 0,3 |
| 0,6 | 0,4 |
| 0,5 | 0,5 |
| 0,4 | 0,6 |
| 0,3 | 0,7 |
| 0,2 | 0,8 |
| 0,1 | 0,9 |
| 0 | 1 |
Рассчитаем стандартное отклонение и ожидаемую доходность «портфеля» из долей участия в обоих фермерских хозяйствах (табл.2) и построим эффективную границу допустимого множества (рис.3)
Таблица 2
Расчет стандартного отклонения и ожидаемой доходности.
| s | |
| 14,00% | 10,0% |
| 13,97% | 10,2% |
| 13,96% | 10,4% |
| 13,99% | 10,6% |
| 14,05% | 10,8% |
| 14,13% | 11,0% |
| 14,25% | 11,2% |
| 14,40% | 11,4% |
| 14,57% | 11,6% |
| 14,77% | 11,8% |
| 15,00% | 12,0% |
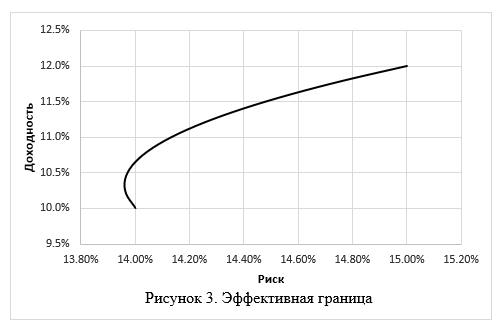
Теорема разделения и сельскохозяйственная диверсификация
Теорема разделения говорит о том, что решение о комбинировании рисковых альтернатив не зависит от объема авансированного капитала и индивидуальной несклонности к риску (подробнее о теореме разделения см, например, в [1], [8]). В дополнение к целевой функции и множеству допустимых фермерских хозяйств для формулировки теоремы в области сельского хозяйства требуется введение дополнительных условий: а) существование безрисковой альтернативы, например, оплата аренды земли наличными; б) возможность приобретения земли по цене, соответствующей доходности безрискового фермерского хозяйства. В этих условиях теорема разделения для сельского хозяйства формулируется следующим образом: оптимальная стратегия для комбинирования рисковых альтернатив не зависит от соотношения количества земли в рисковых фермерских хозяйствах и количества собственной земли.
Если обозначить S* часть общей площади земли S, приходящуюся на рисковые фермерские хозяйства, а S** — площадь дополнительной земли, приобретаемой по безрисковой ставке Rf для увеличения доли рисковых фермерских хозяйств[1], то общая чистая доходность на один гектар будет получаться как
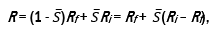
где
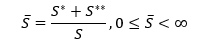
Величина отражает структуру фермы с точки зрения рисковых и безрисковых сельскохозяйственных альтернатив. Если часть земельного участка относится к безрисковой альтернативе, то меньше единицы (S* < S и S** = 0). Если площадь земли, относящейся к рисковой альтернативе, в точности равно площади предоставленного в пользование земельного участка, то величина равна единице (S* = S и S** = 0). Если в дополнение к предоставляемой в пользование земле приобретается земля для рисковых фермерских хозяйств, то больше единицы (S* = S и S** > 0). Используя выражение для R, можно записать математическое ожидание и дисперсию как
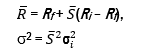
По аналогии с линией рынка капитала в портфельном анализе (см., например, [3]) можно записать выражения для прямой линии, которую будем называть линией рыночных возможностей (MOL – Market Opportunity Line):
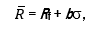
где
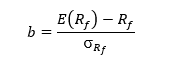
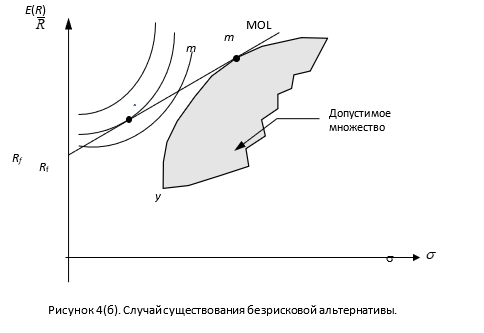
Предположим, фермер выбирает стратегию из допустимого множества, которая максимизирует значение b. Поскольку допустимое множество является строго вогнутым, точка касания его с наивысшей кривой безразличия будет единственной и лежать на эффективной границе. Линия рыночных возможностей, соответствующая этой стратегии, будет находится целиком над допустимым множеством и, таким образом, выше любой другой MOL, соответствующей другой альтернативе. Точки на этой линии определяются как альтернативные значения . Таким образом, решение управления фермы, касающееся рисковых фермерских хозяйств, может рассматриваться с двух точек зрения: а) выбор рискового набора фермерских хозяйств, который максимизирует наклон линии рыночных возможностей; б) при данной MOL – выбор количества земли, которое будет соответствовать рисковым фермерского хозяйствам, или, с другой стороны, величины . Если обозначить m точку касания MOL с допустимым множеством, соответствующую набору рисковых альтернатив, то оптимальная стратегия графически определяется в точке A аналогично портфельному анализу (в случае отсутствия безрисковой альтернативы — рис.4(а), в случае существования безрисковой альтернативы – рис. 4(б)).
С помощью некоторого дополнения к исследованию, представленному выше, можно проанализировать три варианта основной задачи сельскохозяйственной диверсификации: а) допущение различных ставок процента аренды земли; б) рассмотрение задачи сельскохозяйственной диверсификации в долгосрочной перспективе; в) предположение дополнительных ограничений задачи.
Рассмотрение первого варианта приводит к следующей задаче. Пусть R1 – ставка, по которой приобретается дополнительная земля для участия в рисковых фермерских хозяйствах, больше ставки R2, по которой фермер может сдавать в аренду собственную землю.[2] В этом случае мы будем получать две линии рыночных возможностей со следующими уравнениями: 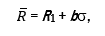
где
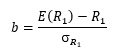
и
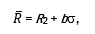
где
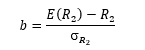
Соответственно, выражение для R1 отражает MOL для фермера, который использует дополнительную землю помимо той, которую ему первоначально предоставили, а выражение для R2 отражает MOL для фермера, который выбирает вариант, когда он сдает в аренду часть предоставленной ему земли. В результате мы получим две точки касания наивысших кривых безразличия с допустимым множеством, и целый отрезок возможных оптимальных стратегий. Длина этого отрезка эффективной границы является функцией от наклона эффективной границы и разности между ставками процента.
Второй вариант характеризуется тем фактом, что в связи с длительной перспективой собственность на землю может изменяться. В этой ситуации приемлемо определять предоставление земли в аренду фермеру как специфический авансированный капитал. Тогда определение оптимального сочетания фермерских хозяйств подразумевает применение теоремы разделения в том виде, как она формулируется в портфельном анализе. Инвестиционные возможности включают доходность как от собственной, так и от арендованной земли. Доходность безрисковой альтернативы – это доходность капитала, помещаемого, например, в краткосрочные облигации. В связи с этим можно сделать вывод о том, что этот вариант может использоваться для определения комбинации арендуемой и собственной земли.
Согласно третьему варианту в рассмотрение могут быть включены дополнительные факторы, такие как государственные программы распределения урожая и бюджетные ассигнования на него, определение порядка севооборота, изменение количества факторов производства. Включение этих дополнительных факторов изменяет эффективную границу таким образом, что MOL, соответствующая максимальному значению b, имеет с ней только одну точку касания, и только одна стратегия может использоваться.
Заключение
Мы рассмотрели возможность применения методов портфельного анализа для решения проблем, связанных с распределением средств по различным земельным участкам для выращивания сельскохозяйственных культур. Было показано, что задача выбора оптимальной комбинации фермерских хозяйств может интерпретироваться как особый случай задачи выбора портфеля. На условном примере мы показали, как выглядит эффективная граница для двух рисковых фермерских хозяйств. Основной вывод заключается в том, что теорема разделения для портфеля ценных бумаг может применяться для решения задач сельского хозяйства.
[1] И S*, и S** не могут принимать отрицательные значения
[2] Случай, когда R1 < R2, не рассматривается, поскольку он означает возможность арбитража
Библиографический список
1. Воронцовский А.В. Инвестиции и финансирование: методы оценки и обоснование. – СПб.: Изд-во СПбГУ, 2003. – 528 с.2. Ивасенко А.Г. Рынок ценных бумаг: инструменты и механизмы функционирования. – М.: Кнорус, 2017. – 272 с.
3. Коростелева М.В. Анализ предпосылок модели оценки финансовых активов // Вестник СПбГУ. Серия: экономика. – СПб: Изд-во СПбГУ. – 2000. – N 3. – С. 100-106.
4. Коростелева М.В. Методы анализа рынка капитала. – СПб: Питер, 2003. – 144 с.
5. Лялин В.А. Рынок ценных бумаг. – М.: ПРОСПЕКТ, 2014. – 383 с.
6. Markowitz H.M. Mean-variance analysis in portfolio choice and capital market. – Oxford; N.Y.: Blackwell, 1987. – 387 p.
7. Markowitz H.M. Portfolio selection // Journal of Finance. – 1952. – Vol.7, N 1. – P. 77-91
8. Tobin J. Liquidity preference as a behavior toward risk // Rev. Econom. Stud. – 1958. – Vol.25, N 6. – P. 65-86.
9. Tobin J. The theory of Portfolio selection // Theory of interest rates / Ed. by F.H. Hahn, F.P.R. Brechling. – London: MacMillan, 1965. – P. 3-51.
