Использование квадратичного программирования для решения задач оптимизации использования молока и молочных продуктов в регионе
Using quadratic programming to solve problems of optimization of use of the milk and dairy products in the region
Abstract: The article is devoted to the application of methods of mathematical programming for the solution of the problems associated with excess milk produced. Under the process of agricultural activities there is a frequent question as to how much milk should be divided between milk for consumption, butter and cheese, and what prices (the policy tool) should then maximize revenues and at the same time minimize dairy subsidies to farmers. Some not very large agricultural enterprises (for example, small farms) may be faced with the fact that milk production can exceed demand if milk prices are set at a level that covers the cost of production. Long-term market equilibrium can not persist in a short period without disturbing social equilibrium. Therefore, it is necessary to find such an optimal possible short-term policy that would determine the structure of the existing market equilibrium. The article realizes two goals. On the one hand, it mentions a very relevant subject of research, the results of which can have a significant impact on future political or economic decisions. On the other hand, it is an illustration of quadratic programming methods, since revenue is supposed to be maximized, which can be written down as a quadratic function of product prices. The article shows the possibility of using these methods, and on the hypothetical example, the extremal problem of optimizing the use of milk and dairy products is solved.
Keywords: milk, butter, cheese, income, price, quadratic programming, optimization problem.
Введение
Предположим, мы имеем дело с одним небольшим регионом, который не имеет авиасообщения, самая дальняя возможная железнодорожная перевозка занимает максимум четыре часа, и не существует внутрирегиональной специализации в производстве молока. Региональный рынок рассматривается как один рынок. Экспортный рынок является отдельным рынком.
Предположим также, что фермеры сами не занимаются продажей молока, а поставляют всё молоко, которое им самим не нужно, на молокозавод. Молокозавод стремится получить максимум дохода от молока, продавая его в чистом виде для потребления, и производя из него масло, сыр, сгущенное молоко и пр., и продавая эти продукты на домашнем и экспортном рынках. Общая стоимость этих продаж молока и продуктов из него, деленная на общее количество молока, поставляемого фермерами, дает среднюю стоимость литра молока. В обмен на это молокозавод гарантирует фермерам определенную цену. Если гарантированная цена выше, чем фактическая средняя цена, молокозавод платит разницу в виде субсидии фермерам. Молокозавод может рассматриваться как монополист с полной властью установления цен и для потребителей, и для поставщиков. В данной статье мы предполагаем, что количество производимого молока фиксировано и задано, поскольку оно может быть точно спрогнозировано. Поскольку процесс максимизации выручки может привести к очень высоким, социально неприемлемым ценам, добавляется «социальное» ограничение, которое приводит к определенной потере полезности, обозначенной нами n.
Материалы и методы
Главными молочными продуктами являются молоко для потребления, масло и различные виды сыра. Мы будем рассматривать два вида сыра – жирный и 40%-ный. В табл. 1 показаны их составляющие.
Таблица 1
Содержание жира, сухого вещества и воды в молоке, масле и сыре, %.
| Жир | Сухое вещество | Вода | Итого | |
| Молоко | 4,1 | 7,9 | 88,0 | 100 |
| Молоко для потребления | 3,1 | 7,9 | 89,0 | 100 |
| Масло | 79,0 | 2,0 | 19,0 | 100 |
| Жирный сыр | 29,9 | 30,1 | 40,0 | 100 |
| 40% сыр | 23,8 | 38,2 | 38,0 | 100 |
Общее наличие жира и сухого вещества определяется общим количеством производимого сырого молока (допустим, 7 123 000 тонн). В табл. 2 представлены результаты вычетов из произведенного молока, и конечное общее количество жира в 154 000 тонн и сухого вещества в 227 000 тонн. Вычеты сделаны для фермерского использования, экспорта масла, сыра и молока, и производства специальных продуктов, которые должны экспортироваться.
Таблица 2
Имеющееся количество жира и сухого вещества (в 1000 тонн)
| Жир | Сухое вещество | |
| Продукты из произведенного молока (7 123 x содержание) | 292 | 563 |
| 1. Фермерское использование молока для скота | 12 | 55 |
| 2. Фермерское использование молока для потребления | 14 | 34 |
| 3. Экспорт масла | 33 | 2 |
| 4. Экспорт жирного сыра | 21 | 19 |
| 5. Экспорт 40%-го сыра | 9 | 13 |
| 6. Экспорт молока | 4 | 12 |
| 7. Специальные продукты: сгущенное молоко | 29 | 98 |
| 8. Специальные продукты: сухое молоко | 16 | 103 |
| Итоговые вычеты | 138 | 336 |
| Доступно продуктов из молока | 154 | 227 |
На основании этих данных можно сформулировать следующие ограничения на производство молока, масла и сыра: обозначив x1, x2, x3, и x4 количества в 1000 тонн произведенного молока, масла, жирного сыра и 40%-го сыра соответственно, мы получим:
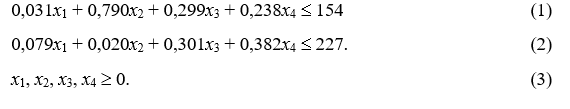
Определение функций спроса представляет собой аппроксимацию. Аппроксимация обычно касается формы выбранной конкретной функции, а также численной спецификации параметров выбранной функции.
Наши функции спроса основаны на трех множествах данных: фактического количества потребленного молока, масла и сыра, обозначаемого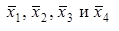 ;
;
их (средней) цены 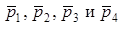 ;
;
и различной эластичности и перекрестной эластичности, обозначаемой e.
Эти последние значения основаны на существующем изучении поведения потребителя. Предполагается, что функции линейны:[1]

Таким образом, общая выручка равна 91,8 млн рублей. Можно также отметить, что наличие жира, как дано выше, несколько превосходит необходимое его количество для удовлетворения этого спроса; (небольшое) различие является результатом изменений в запасах, а также ошибками измерения.
Значения эластичности и перекрестной эластичности:

В соответствии с теорией потребления перекрестная эластичность е34 была взята в размере, меньшем по сравнению с е43 в пять раз, поскольку бюджетная квота жирного сыра примерно в пять раз превышает бюджетную квоту 40%-ного сыра (см. (8)). Подставляя (8) и (9) в (4) – (7), получим четыре линейные убывающие функции спроса:
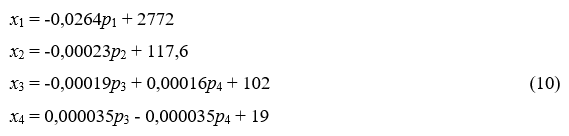
Для небольших отклонений от первоначальных значений эти функции будут, вероятно, являться хорошей аппроксимацией. С увеличением отклонений результаты должны будут интерпретироваться более аккуратно. Очевидно, могут быть рассмотрены различные значения параметров.
Функция, которую мы максимизируем, представляет собой выражение . Используя выражение (10), целевую функцию можно переписать как квадратичную функцию от pi (об использовании квадратичного программирования в сельском хозяйстве см., например, [3]). Ее максимум достигается при следующих значениях цен и количества продуктов:
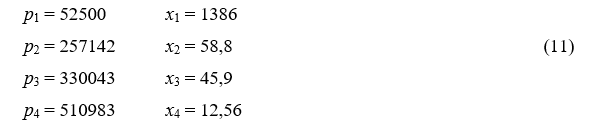
Это решение удовлетворяет ограничениям (1), (2) и (3). Общая выручка в этом случае равна 109,5 млн рублей; чистая прибыль составляет около 17,7 млн рублей, но этого не вполне достаточно, чтобы покрыть ежегодные субсидии фермерам.
Сильное ценовое увеличение является неприемлемым с социальной точки зрения, поэтому должно быть добавлено следующее ограничение:
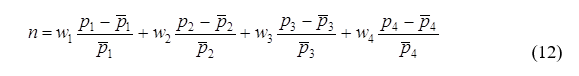
В выражении (12) коэффициенты wi представляют собой веса, присвоенные отклонениям от первоначальной (за 2015г.) цены. Ценовая структура в 2015г. принята за «нормальную»[5]. Веса wi были определены таким образом, что приблизительно выполняется следующее соотношение:
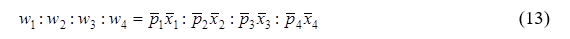
Предположим, взвешивание дало следующие значения, в сумме равные 10:
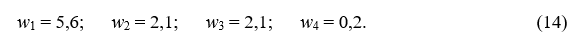
Это означает, что, если все цены увеличиваются на 1 процент, n = 1/10. Значение n является нулевым в исходной ситуации, и остается нулевым до тех пор, пока соответствующие средневзвешенные значения относительных ценовых изменений остаются равными нулю. В этом смысле значение n, равное нулю, может быть названо нейтральным. По мере того, как оно растет относительно нуля, с социальной точки зрения становится все хуже.
Подставляя значения из выражений (14) и (8) в (12), мы получим:
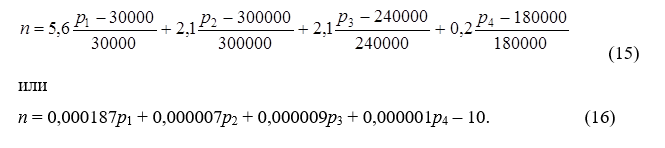
Результаты и обсуждение
Таким образом, может быть поставлена следующая задача: максимизировать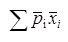 для различных значений n, определив цены при данных доступных количествах продуктов, при данных функциях спроса (10) и при условии выполнения ограничений (1), (2), (3) и (16).
для различных значений n, определив цены при данных доступных количествах продуктов, при данных функциях спроса (10) и при условии выполнения ограничений (1), (2), (3) и (16).
Поскольку инструментами в данном случае являются цены, нам необходимо переформулировать ограничения (1) и (2) с использованием переменных pi, а не xi. Это можно сделать, подставляя (10) в (1) и (2):

Сюда же добавляем социальное ограничение (16), полагаем n = 0, а целевую функцию, максимизирующую общую выручку, записываем как квадратичную функцию от pi:
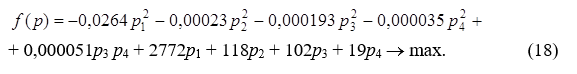
Решая задачу квадратичного программирования (16)-(18), мы получим следующие результаты: общая выручка равна 97,3 млн рублей, оптимальный план p* = (35419; 183191,5; 197811; 337743), вектор переменных x = (1837; 75,7; 68,7; 14) (о методах решения подобных задач см., например, [2], [4], [6], [8]), о реализации методов решения оптимизационных задач в среде MS Excel подробно говорится в [1]). Заметим, что общая выручка получается ненамного больше полученной на практике — 91,8 млн рублей. Дополнительный доход в размере 5,5 миллионов рублей получается путем увеличения цены молока и масла, и снижения цены сыра. В табл.3 представлено решение для разных значений n. Абсолютный максимум достигается при значениях, указанных в (11), и n = 5,05564.
Таблица 3
Оптимальные решения при различных значениях n.
| n | 0 | 1 | 2 | 3 | 4 | 5 | 5,05564 | 6 |
| p1 | 35418,99 | 38797,588 | 42176,191 | 45554,795 | 48933,396 | 52312,05 | 52499,936 | 55690,657 |
| p2 | 183191,5 | 197818,95 | 212446,44 | 227073,92 | 241701,43 | 256329,1 | 257142,55 | 270956,6 |
| p3 | 197810,9 | 223966,48 | 250121,97 | 276277,46 | 302433,01 | 328588,82 | 330043,34 | 354744,34 |
| p4 | 337743 | 372009,88 | 406276,77 | 440543,72 | 474810,54 | 509077,97 | 510983,57 | 543344,9 |
| x1 | 1836,939 | 1747,7437 | 1658,5485 | 1569,3534 | 1480,1584 | 1390,9619 | 1386,0017 | 1301,7667 |
| x2 | 75,71021 | 72,365399 | 69,02058 | 65,675764 | 62,33094 | 58,98608 | 58,80007 | 55,641257 |
| x3 | 68,69797 | 64,193307 | 59,688657 | 55,184007 | 50,679343 | 46,17464 | 45,924134 | 41,669984 |
| x4 | 14,00238 | 13,718481 | 13,434582 | 13,150681 | 12,866786 | 12,58288 | 12,567092 | 12,298981 |
| f(p) | 97250389 | 101604084 | 105002040 | 107444373 | 108931057 | 109462053 | 109463532 | 109037399 |
Выводы
- результаты основаны на функциях спроса (которые являются наилучшей аппроксимацией) и социальном ограничении (которое является произвольным);
- цены близки к их оптимальным значениям, только если рассматриваются социально нейтральные случаи;
- по мере возрастания n цены поднимаются так высоко, что спрос больше не является достаточным, чтобы можно было полностью использовать молочный жир.
[1] Для больших положительных отклонений от равновесных цен это будет, вероятно, сказываться на недооценке спроса и, следовательно, дохода.
Библиографический список
1. Грызина Н.Ю., Мастяева И.Н., Семенихина О.Н. Математические методы исследования операций в экономике: Учебно-методический комплекс. – М.: Изд. центр ЕАОИ, 2008. – 204c.2. Конюховский П.В. Математические методы исследования операций в экономике. – СПб: Изд-во СПбГУ, 2008. – 394с.
3. Коростелева М.В. Экономико-математическое моделирование сельскохозяйственной деятельности в условиях риска // Аэкономика: экономика и сельское хозяйство, 2017. №2 (14). URL: http://aeconomy.ru/science/economy/ekonomiko-matematicheskoe-modelirov/
4. Математические методы и модели исследования операций / В. А. Колемаев, Т. М. Гатауллин, Н. И. Заичкин и др. – М.: ЮНИТИ, 2009. – 591с.
5. Сельское хозяйство, охота и охотничье хозяйство, лесоводство в России. 2015: Стат.сб. / Росстат – M., 2015. – 201 c.
6. Таха, Х. А. Введение в исследование операций: – М.: Издательский дом «Вильямс», 2005. – 901с.
7. Agricultural Finance. From Crops to Land, Water and Infrastructure. / H.Geman. – NJ: Wiley, 2015. – 291 p.
8. Operations Research. A Model-Based Approach. H. A. Eiselt, C.-L. Sandblom. – Springer Berlin Heidelberg, 2010. – 447 p.
