Введение

Вопросы повышения эффективности производства являются неотъемлемой частью развития экономических систем. Пути повышения производства и критерии, с помощью которых определяется сама эффективность производства, базируются на различных показателях. Одним из таких показателей является предельная эффективность использования ресурсов в производстве.

Линейное программирование как метод анализа задачи об использовании ресурсов в производственном процессе

Вопросы связи полезности ресурсов в производственном процессе с их количествами, которые используются в производстве, успешно исследуются с помощью математических моделей и методов. Одним из таких направлений является использование методов линейного программирования, с помощью которых строятся модели и проводится анализ использования ресурсов в производстве. В статье строится модель предприятия, использующего три ресурса и выпускающего два вида продукции. Один из ресурсов имеет фиксированный запас, а для двух других ресурсов предполагается, что их объёмы в использовании в производстве изменяются. Сама задача по использованию ресурсов представляется как задача линейного программирования, с помощью которой проводится анализ использования ресурсов.

Сформулируем задачу по исследованию предельных полезностей ресурсов в общем виде. Рассматривается предприятие, на котором производится n видов продукции А₁, А₂, …, А_n. Для производства продукции предприятие использует m ресурсов R₁, R₂, …, R_m. Заданы нормы затрат ресурсов по каждому виду продукции, запасы ресурсов, имеющихся в распоряжении предприятия, а также стоимости реализованной продукции, изготовленной предприятием. Предполагается, что ресурсы разделены на две категории: первая категория состоит из ресурсов, запасы которых фиксированы, не изменяются, а во второй категории все ресурсы имеют изменяемые объёмы запасов на предприятии.

Определить зависимость предельных полезностей всех ресурсов от запасов ресурсов, объёмы которых изменяются, при условии максимизации стоимости реализованной продукции, изготовленной на предприятии.

Дефицитные и избыточные ресурсы

Для решения поставленной задачи будем использовать свойства ресурсов, их дефицитность и избыточность.

Ресурс будем называть дефицитным, если его предельная полезность при заданных запасах на предприятии отлична от нуля. Отметим, что понятие предельной полезности ресурса предполагает его полезность для производства при оптимальном плане. Также полезность использования ресурса в производстве называют двойственной оценкой использования ресурса. Для дефицитных ресурсов их остаток при оптимальном плане равен нулю.

Ресурс будем называть избыточным, если при оптимальном плане его остаток строго больше нуля. Предельная полезность такого ресурса равна нулю, а ограничение в прямой задаче для этого ресурса выполняется как строгое неравенство.

Использование графического способа для определения предельной полезности ресурсов

Для решения поставленной задачи будем использовать свойство ресурсов быть избыточными. Использование избыточности ресурса даёт возможность исследовать двойственную задачу об использовании ресурсов, так как предельная полезность такого ресурса равна нулю.

Кроме свойства избыточности ресурсов используем критерий для видов продукции, по которому продукцию невыгодно выпускать, если его двойственная оценка способа производства не равна нулю. В этом случае для предельных полезностей ресурсов будет выполнятся условие в виде неравенства, что даст возможность решать вырожденные прямые задачи при определении предельных полезностей используемых ресурсов.

Кроме того, условие избыточности ресурсов определяет условия для объёмов изменяющихся ресурсов в виде неравенств. Эти условия задают области в пространстве меняющихся ресурсов, в которых предельные полезности имеют одно аналитическое выражение либо постоянные.

Рассматривая различные варианты избыточности и дефицитности всех ресурсов задачи, пространство для меняющихся ресурсов разобьётся на области, в которых аналитическое выражение предельных полезностей меняться не будет.

Для каждого варианта составим задачу линейного программирования. Так как полагается изначально, что предприятие производит два вида ресурса, то поставленные задачи линейного программирования можно будет решать графическим способом.

Чтобы провести анализ использования ресурсов при конкретном варианте избыточности и дефицитности ресурсов, будем решать двойственную задачу по решению прямой задачи, которую мы решим графическим способом.

Решение задачи будем рассматривать, когда предприятие использует три ресурса, один из которых относится к первой категории, а второй и третий к третьей категории. Для определённости в качестве первого ресурса будем рассматривать сырьё, в качестве второго оборудование, а в качестве третьего трудовые ресурсы.

Чтобы не запутаться в вариантах принадлежности ресурсов по их свойствам, используем следующую последовательность, в которой будут рассматриваться ресурсы.

1) Сырьё и трудовые ресурсы избыточные, оборудование дефицитный ресурс;

2) Сырьё и оборудование избыточные ресурсы, трудовые ресурсы дефицитный ресурс;

3) Оборудование и трудовые ресурсы избыточные, сырьё дефицитный ресурс;

4) Сырьё избыточный ресурс, оборудование и трудовые ресурсы дефицитные;

5) Трудовые ресурсы избыточные, сырьё и оборудование дефицитные;

6) Оборудование избыточное, сырьё и трудовые ресурсы дефицитные;

7) Все ресурсы дефицитные.

4. Решение задачи об использовании ресурсов, когда запас сырья задан, а запасы оборудования и трудовых ресурсов изменяются

Пример 1. Для изготовления продукции двух видов А и Б предприятие расходует ресурсы, а от реализации этой продукции получает доход. Информация о нормах затрат ресурсов на единицу выпускаемой продукции, запасах расходуемых ресурсов, имеющихся в распоряжении предприятия, и стоимость реализованной продукции приведены в таблице 1.

Таблица 1.

Нормы затрат ресурсов, их запасы и стоимость реализованной продукции

Определить зависимость предельных полезностей

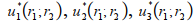, сырья, оборудования и трудовых ресурсов от количеств оборудования и трудовых ресурсов , используемых в производстве.

Решение. 1) Для решения задачи построим её экономико-математическую модель. Определим для модели переменные: х₁ – объём выпуска продукции вида А, х₂ – объём выпуска продукции вида Б. В качестве целевой функции модели возьмём величину Z – выручка предприятия. Выразим основные условия и ограничения задачи в математической форме. Первое условие: 3х₁+х₂ ≤ 222 – ограничение на потребление сырья; второе условие: х₁+3х₂ ≤ r₁ – ограничение на использование оборудования; третье условие: 7х₁+х₂≤r2 – ограничение на использование трудовых ресурсов. По умолчанию полагаем, что количества выпускаемой продукции неотрицательные: х₁≥0, х₂≥0. Целевая функция равна: Z= 201х₁+ +187х₂.

Построим экономико-математическую модель задачи: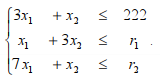

Определяем для неё двойственную задачу для расчёта оценки предельной полезности ресурсов.

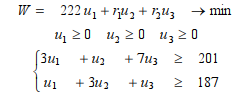
4.1. Решение задачи, когда сырьё и трудовые ресурсы будут избыточными

Полагаем, что избыточными будут сырьё и трудовые ресурсы. Тогда r₁ принимает такие значения, что при оптимальном плане остаток оборудования будет равен нулю (y₂*=0), а остатки сырья и трудовых и ресурсов будут строго больше нуля (y₁*>0, y₃*>0).

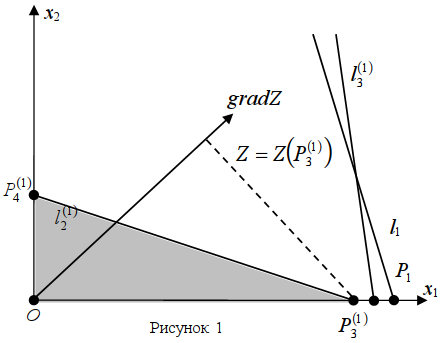Решим задачу при этих условиях графически (рис. 1). Строим ОДР: ОДР= (рис.1).   Решением задачи будет точка  (рис. 1), которая является точкой пересечения оси Ох1 и прямой  . Для точки  справедливы условия: х1*> 0 и х2*=0. Найдём координаты точки :

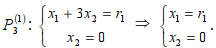Получаем, что оптимальное решение будет Х*=(r1;0). Значение целевой функции в этом случае равно: Zmax=201∙r₁ руб. Остатки ресурсов для этого плана: у*1=222–3r1>0; y*2=0; y*3=r2 –7r1 >0.

Решение двойственной задачи при этих условиях на r₁ определим из решения прямой задачи. Так как,  у*₁ > 0 и у*₃ > 0, то u*₁=u*₃=0. Так как x*₁ >0, то v*₁= 0. Отсюда следует, что 3•0+u₂*+7•0=201  u₂*=201. Расширенное решение задачи:

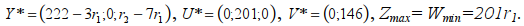
Определяем область D₁ на плоскости, которая соответствует условиям задачи:

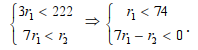
Построим область D₁ на плоскости О_r1r2 (рис.2).

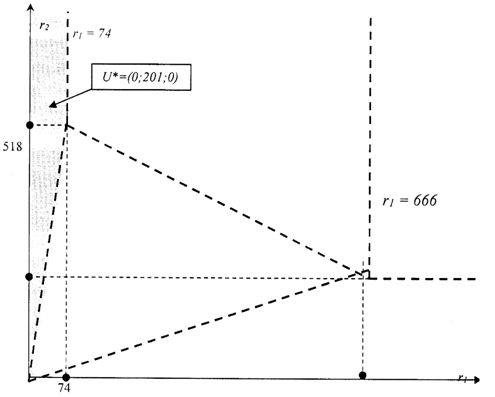
4.2. Решение задачи, когда избыточные сырьё и оборудование

Теперь рассмотрим случай, когда избыточными будут сырьё и оборудование. Тогда _r2 принимает такие значения, что трудовые ресурсы будут дефицитным ресурсом (y₂*=0), а y₁*>0, y₃*>0

Решаем задачу при этих условиях графически (рис. 1). Строим ОДР: ОДР=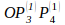(рис.1). Решением задачи будет точка (рис. 1), которая является точкой пересечения оси Ох1 и прямой 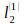. Для точки 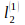справедливы условия: х₁*> 0 и х₂*=0. Найдём координаты точки :

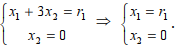
Получаем, что оптимальное решение будет Х*=(r₁;0). Значение целевой функции в этом случае равно: Zmax=201∙r₁ руб. Остатки ресурсов для этого плана: у*₁=222–3r₁>0; y*₂=0; y*₃=r₂ –7r₁ >0.

Решение двойственной задачи при этих условиях на r₁ определим из решения прямой задачи. Так как, у*₁ > 0 и у*₃ > 0, то u*₁=u*₃=0. Так как x*₁ >0, то v*₁= 0. Отсюда следует, что 3·0+u₂*+7·0=201 u₂*=201. Расширенное решение задачи:

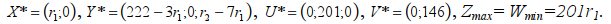
Определяем область D₁ на плоскости, которая соответствует условиям задачи:

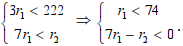
Построим область D₁ на плоскости О_r1r2 (рис.2).

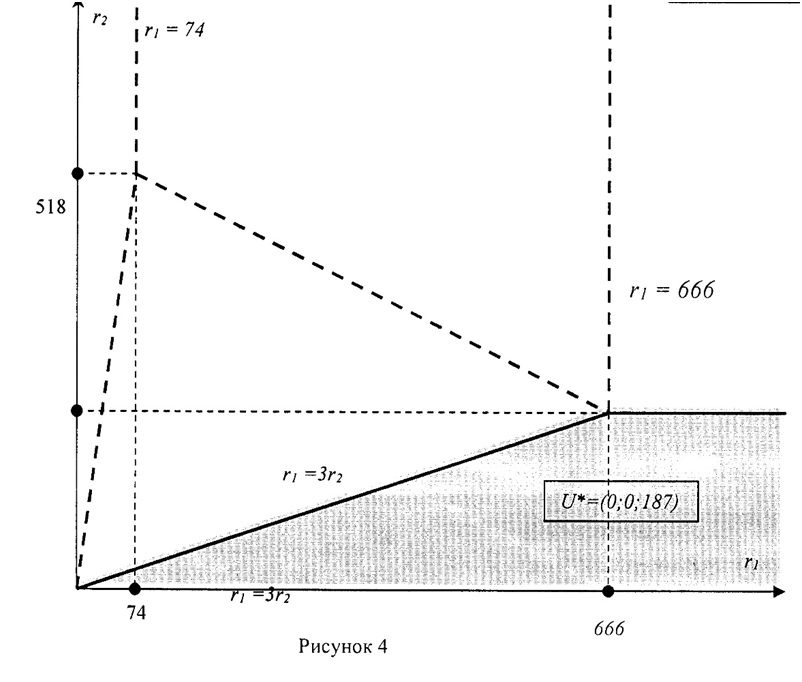
4.3. Избыточные оборудование и трудовые ресурсы

Переходим к случаю, когда r₁ и r₂ принимают такие значения, что сырьё будет дефицитным ресурсом, а оборудование и трудовые ресурсы будут избыточными. Тогда ОДР будет ограничена прямой и осями координат: ОДР=ОP₁P₂. Этому случаю могут соответствовать и другие ОДР, их мы будем рассматривать в других вариантах наличия свойства избыточности ресурсов и при необходимости сделаем корректировку.

Решением задачи будет точка P₂ (рис. 5), точка пересечения оси Ох2 и прямой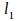

Найдём её координаты: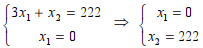

Получаем, что Х*=(0;222). Значение целевой функции в этом случае равно: Z_max=201∙0+187∙222=41514 руб. Определим остатки ресурсов для этого плана: у*₁=0; y*₂=r₁ – 666; y*₃= r₂ – 222.

Найдём решение двойственной задачи. Так как у*₂> 0 и у*₃ > 0, то u*₂=u*₃=0. Так как x*₂ >0, значит v*₂= 0u₁*=187 . Расширенное решение задачи:

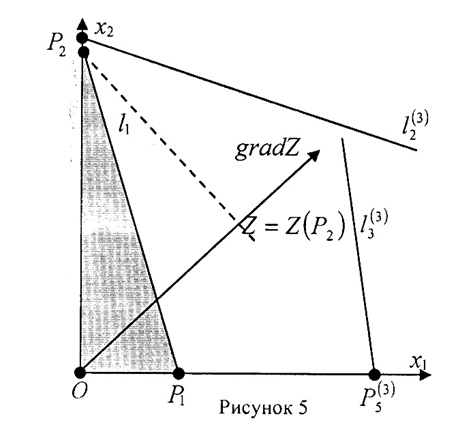
Мы получили решение для области D₃: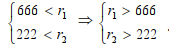 Решение для области D₃: .

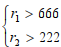Построим область D₃ на плоскости О_r1r2 (рис.6).

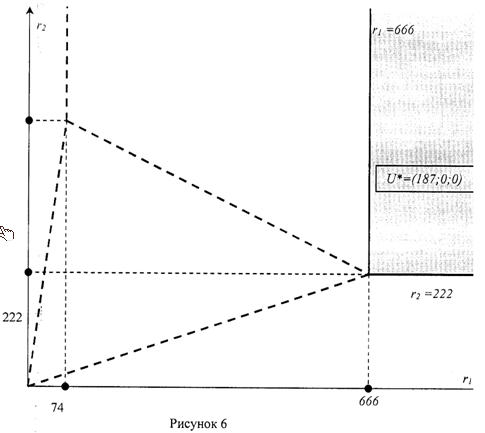
4.4. Сырьё – избыточный ресурс

Рассмотрим случай, когда будет избыточным только один ресурс. Начнём с сырья. Тогда y₁*>0, y₂*=0, y₃*=0.

Для этих условий решим задачу графически (рис.7, 9, 11). ОДР в этих условиях может представляться в трёх видах, в зависимости от того, продукция какого вида выпускается при оптимальном плане, а какая нет. Для каждого случая ОДР оптимальный план будет разным. Последовательно рассмотрим каждую задачу.

1) Пусть выпускается только продукция вида А. Тогда значения оптимального плана х* будут равны: х*₁ ≥0, х*₂=0 (рис. 7). ОДР в этом случае будет треугольник О Р4(5) Р3(5.) Оптимальным будет план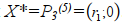 . Записываем условия на r₁ и 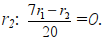Отсюда получаем, что 7r₁=r₂.

Переходим к ограничениям в двойственной задаче при оптимальном плане: 3u₁*+u₂*+7u₃*=201; u₁*+3u₂*+u₃*≥187. Так как u*₁=0, то u₂*+7u₃*=201 и 3u₂*+ u₃*≥187.

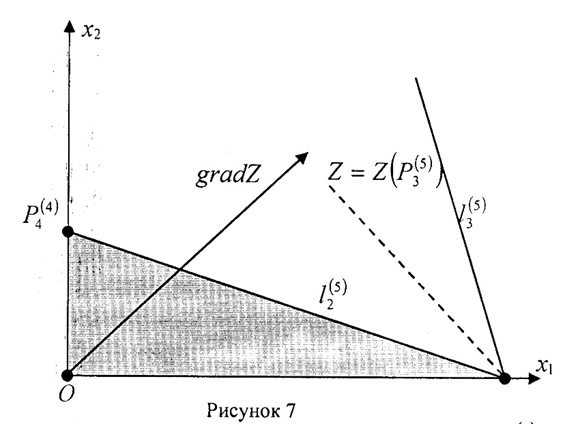
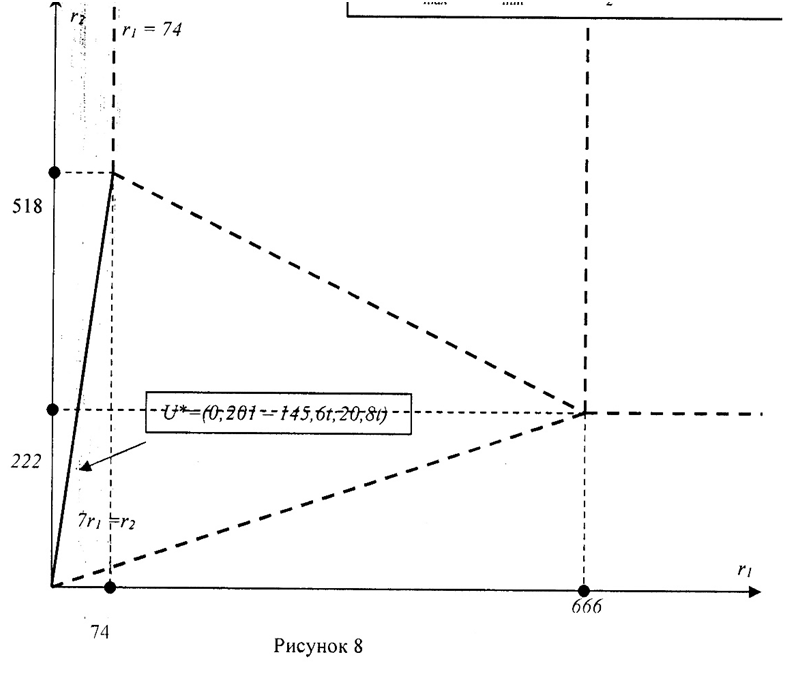
Из уравнения выражаем u₂*: u₂*=201–7u₃*. Подставляем это выражение в неравенство: 3·(201–7u₃*)+u₃*=603 –20u₃*≥ 187 20u₃*≤ 416 u₃*≤20,8. Положим u3*=20,8t, тогда, учитывая, что u₃*≥0, 0 ≤t≤1. Выражаем через t оценку u₂*: u₂*=201–7·20,8t=201–145,6t. Вычислим v*₂: v*₂=3u₂*+ u₃*–187 =3·(201–145,6t)+20,8t–187=603–436,8t+20,8t–187=416–416t, где 0 ≤t≤1.

Расширенное решение задачи: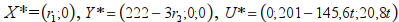 где 0≤t≤1,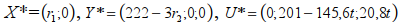, где 0 ≤t≤1, Z_max= Wmin=201r₁.

Определим область D4. Она должна удовлетворять условиям прямой задачи: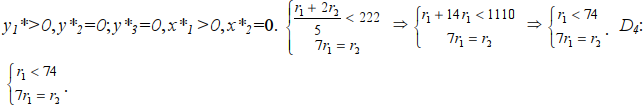

Построим область D₄ на плоскости О_r1r2 (рис.8).

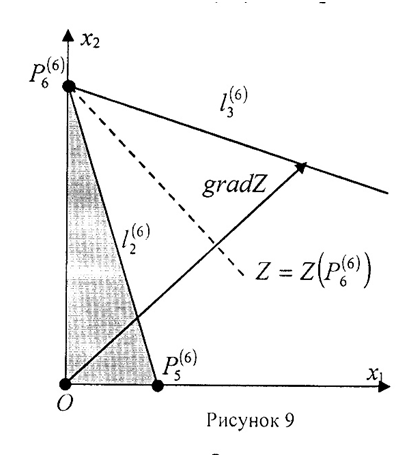
2) Значения х* будут: х*₁=0, х*₂≥0. ОДР в этом случае будет треугольник О Р₆⁽⁵⁾ Р₅⁽⁵⁾. Отсюда получаем условие на r1 и r2: 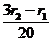= 0. Отсюда получаем, что r₁=3_r2.
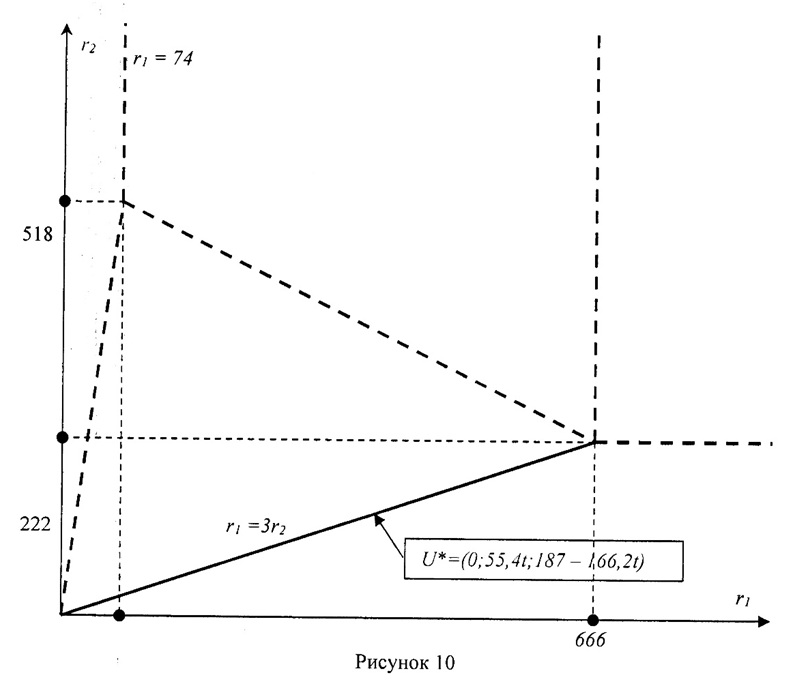
В двойственной задаче: 3u₁*+u₂*+7u₃*≥201; u₁*+3u₂*+ u₃*=187. Так как u*₁=0, то u₂*+7 u₃*≥201 и 3u₂*+ u₃*=187. Из уравнения выражаем u₃*: u₃*=187–3u₂*. Подставляем это выражение в неравенство: u₂*+7·(187–3u₂*)=1309 –20u₂*≥ 201 20u₂*≤ 1108 u₂* ≤ 55,4. Положим u₂*=55,4t, тогда, учитывая, что u₂*≥0, 0 ≤t≤1. Выражаем через t оценку u3*: u3*=187–3·55,4t=187–166,2t. Вычислим v*2: v*1=u₂*+ 7₃*–201=55,4t +7·(187–166,2t ) –201=1307–1163,4t+55,4t –201=1108–1108t, где 0 ≤t≤1.

Расширенное решение задачи:

Определим область D₅. Она должна удовлетворят условиям прямой задачи: y₁*>0, y*₂=0; y*₃=0, х*₁=0, х*₂>0.

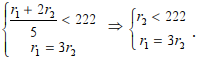Область D₅. определяется системой неравенств:.

Построим область D₅ на плоскости Оr₁r₂ (рис.10).
Отметим, что области D₄ и D₅ будут открытыми интервалами, лежащими на прямых 7r₁=r₂ и r₁=3r₂ на плоскости Оr₁r₂ соответственно (рис. 8 и 10). Для первого интервала 0<r1 <74, для второго интервала 0<r2<222.

3) Пусть при оптимальном плане производятся оба вида продукции. Значения х* будут: х*₁ ≥0, х*₂ ≥0 (рис. 11). ОДР в этом случае будет четырёхугольник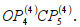

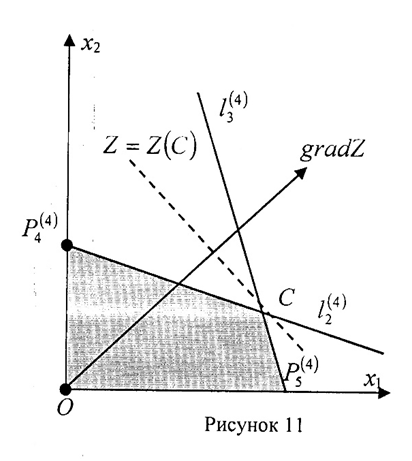
Решением задачи будет точка C (рис. 11), точка пересечения точка пересечения прямых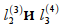. Найдём её координаты: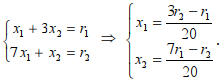

Получаем, что 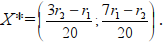Значение целевой функции в этом случае равно:

Переходим к ограничениям в двойственной задаче при оптимальном плане: 3u₁*+u₂*+7u₃*=201; u₁*+3u₂*+ u₃*=187. Так как u*₁=0, то u₂*+7 u₃*=201 и 3u₂*+ u₃*=187. Решаем систему из двух уравнений. Найдём u₂*: 20u₂*=187·7–201=1108 u₂*=55,4. Найдём u₃*: 20u₃*=201·3–187=416 u₃*=20,8.
Расширенное решение задачи:

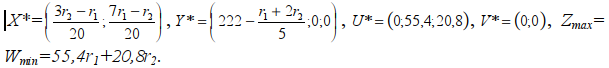
Определим область D₆. Она должна удовлетворят условиям прямой задачи: y₁*>0, y*₂=0; y*₃=0, х*₁ >0, х*₂>0.
. D6 определяется системой неравенств: .
Построим область D₆ на плоскости О_r1r2 (рис.12).

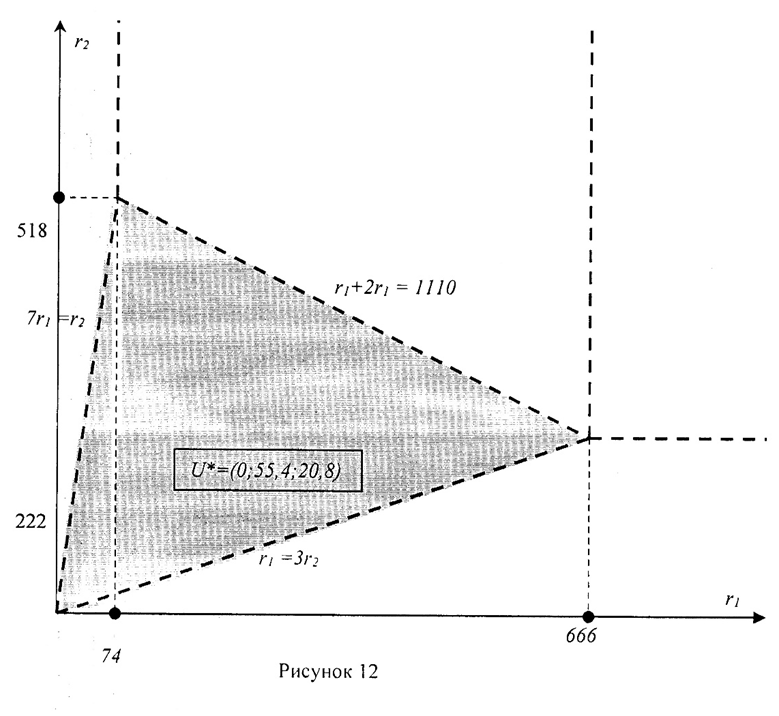
4.5. Трудовые ресурсы – избыточный ресурс

Теперь рассмотрим случай, когда будут избыточными только трудовые ресурсы. Тогда y1*=0, y2*=0, y3*>0. Оптимальное решение в прямо задаче будет удовлетворять системе условий

.

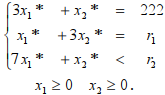Возможные решения этой задачи рассмотрены на рисунках 13, 15 и 17. Во всех этих задачах оптимальные планы разные. Поэтому каждую из задач мы рассмотрим отдельно.
Также рассмотрим три случая для объёмов выпуска продукции при оптимальном плане, оба вида продукции имеют ненулевые объёмы, продукция вида А имеет ненулевой объём, а продукция вида Б – нулевой, и объём продукции вида А нулевой, а продукции вида Б – ненулевой.
1) На рисунке 13 представлено решение, когда объёмы выпускаемых видов продукции отличны от нуля: х*₁ >0, х*₂>0. Найдём оптимальный план как точки пересечения прямых 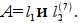. Решаем систему уравнений: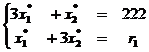. Её решение будет точка Х*=.

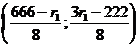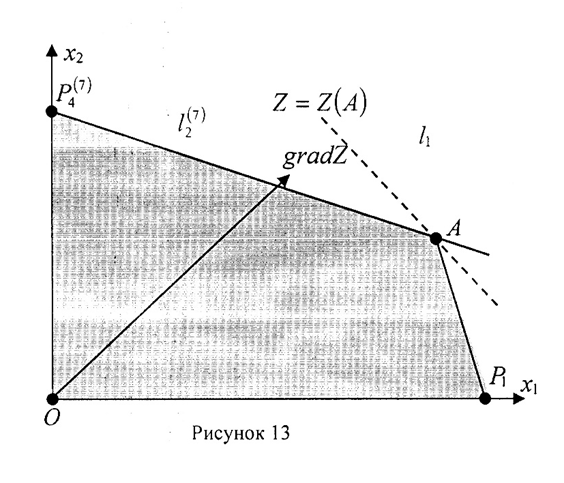
Из неравенства системы определяем условия для r₁ и r₂:

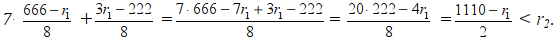
Из условия, что переменные, получаем: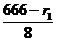> 0, 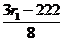> 0. Оптимальное значение целевой функции равно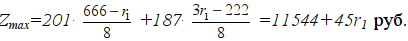

Проверим условия «дополняющей нежёсткости». Так как у*₃ > 0, значит u*₃= 0. Так как х*₁> 0, то v*₁= 0, так как х*₂> 0, то v*₂= 0. Получаем: 3u₁*+u₂*=201; u₁*+3u₂*=187; u*3=0. Решаем систему уравнений: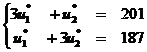 . Её решение будет точка

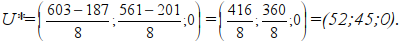
Найдём Wmin: W_min=222·52+45r₂+0 ·r₂ = =11544+45r₂.
Определим область D₇. Она должна удовлетворят условиям прямой задачи: y₁*=0, y*₂=0; y*₃>0, х*₁ >0, х*₂>0.

.

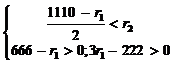D₇ определяется системой неравенств:.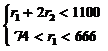

Построим область D₇ на плоскости О_r1r2 (рис.14).

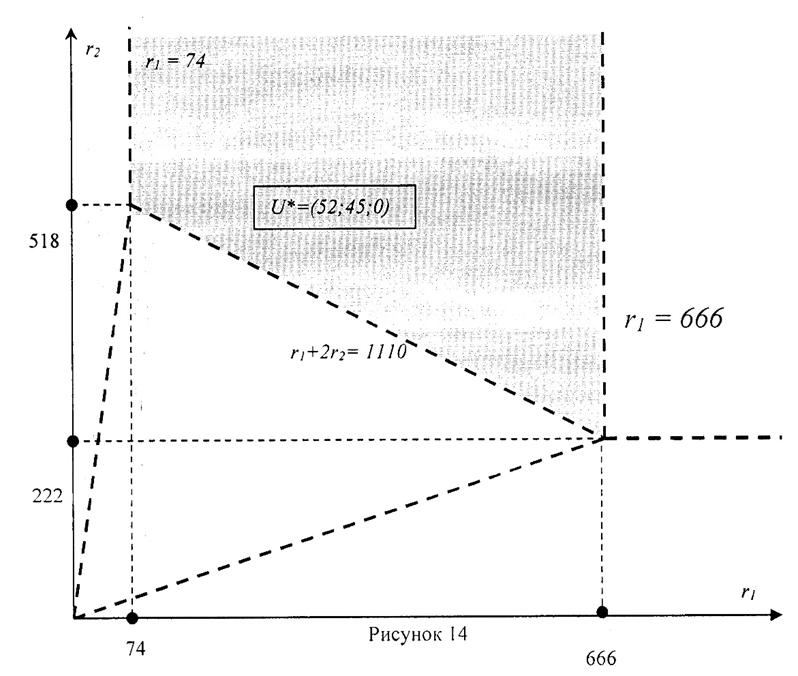
2) На рисунке 15 представлено решение, когда объём продукции вида А отличен от нуля (х*₁ >0), а объём продукции вида Б равен нулю (х*₂=0). Оптимальный план – точка Р₁. Это точка пересечения прямо и оси О_х1. Тогда 3_х1*=222 и х₁*=r₁: Х*= (74;0).

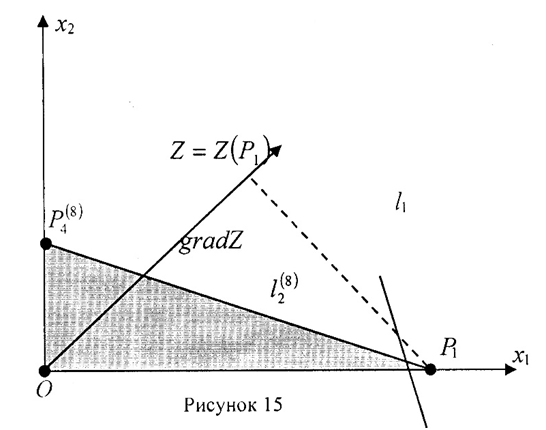
Из неравенства системы определяем условия для r₁ и r₂: 7∙ 74= 518 < r₂. Так как точка Р₁ совпадает с точкой Р₃(8) получаем условие на r₁: r₁=74. Оптимальное значение целевой функции равно Z_max=201∙74 =14874 руб.
Решаем двойственную задачу: 3u₁*+u₂*=201; u₁*+3u₂* ≥187, u*₃=0. Выражаем u₂*: u₂*=201–3u₁*. Подставляем это выражение в неравенство: u₁*+3·(201–3u₁*)=603–8u₁*≥ 187 8u₁*≤ 416 u₁*≤ 52. Положим u₁*=52t, 0 ≤t≤1. Тогда u₂*=201–3·52t u₂*=201–156t. Вычислим v*₂: v*₂=52t +3·(201–156t ) = =603 –416 t, где 0 ≤t≤1. Найдём W_min: Wmin=222·52t+74·(201–156t)+0 ·r₂ =14874.
Определим область D₈. Она должна удовлетворят условиям прямой задачи: y₁*=0, y*₂=0; y*₃>0, х*₁ >0, х*₂=0.

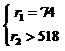. D₈ определяется системой неравенств:.

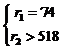Построим область D₈ на плоскости О_r1r2 (рис.16).

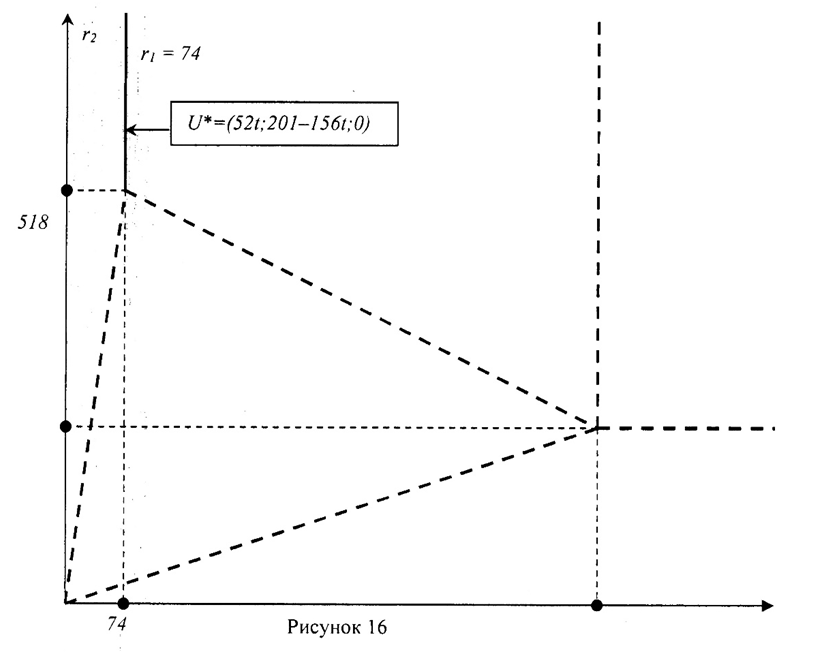
3) На рисунке 17 представлено решение задачи, в котором объём продукции вида А равен нулю (х*₁ =0), а объём продукции вида Б не равен нулю (х*₂>0).

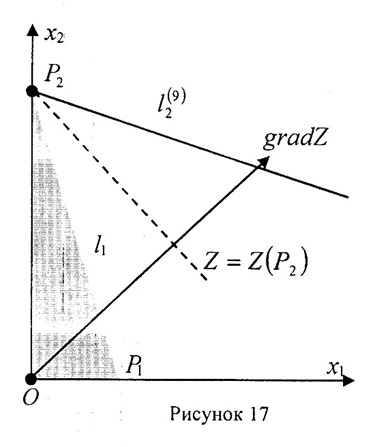
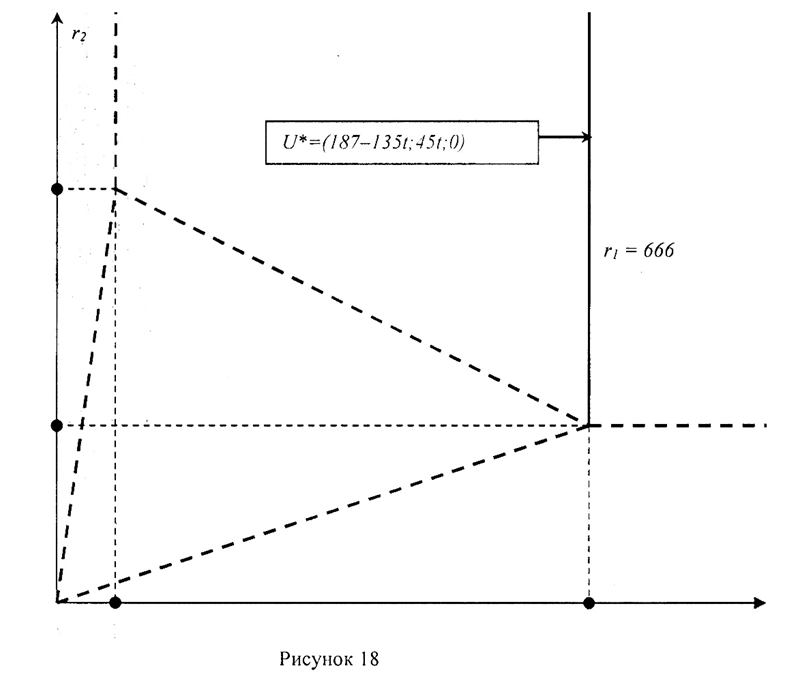
Оптимальный план – точка Р₂. Это точка, в которой пересекаются прямая 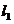и ось О_х2. Тогда х₂*=222 и 3х₁*=r₁: Х*= (0;222).
Из неравенства системы определяем условия для r₂:222<r₂. Так как точка Р₂ совпадает с точкой Р₄⁽⁹, то получаем условие на r₂: r₂=222. Оптимальное значение целевой функции равно Z_max=187∙222 =41514 руб.
Решаем двойственную задачу: 3u₁*+u₂*≥201; u₁*+3u₂*=187, u*₃=0. Выражаем u₁*: u₁*=187–3u₂*. Подставляем это выражение в неравенство: 3·(187–3u₂*)+u₂=561–8u₂*≥ 201 8u₂*≤ 360 u₂*≤ 45. Положим u₂*=45t, 0 ≤t≤1. Тогда u₁*=187–3·45t u₁*=187–135t. Вычислим v*₁: v*₁=3·(187–45t )+45t–201= 360–416t, где 0 ≤t≤1. Найдём W_min: W_min=222·(187–135t)+666·45t +0 ·r₂ = 41514.
Определим область D₉. Она должна удовлетворят условиям прямой задачи: y₁*=0, y*₂=0; y*₃>0, х*₁ =0, х*₂>0. Получаем:.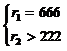

D9 определяется системой неравенств:.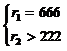
Построим область D₉ на плоскости О_r1r2 (рис.18).

4.6. Избыточный ресурс — оборудование

Рассмотрим случай, когда будет избыточным только оборудование. Тогда y₁*=0, y₂*>0, y₃*=0.
Тогда оптимальное решение в прямо задаче будет удовлетворять системе условий.

Возможные решения этой задачи рассмотрены на рисунках 19, 20 и 21. Во всех этих задачах оптимальным будет план 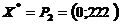. Из первого уравнения и второго неравенства системы определяем условия для r₁ и r₂: 3r₂< r₁, r₂=222. Оптимальное значение целевой функции равно Z_max=201∙0+187∙222=41514 руб.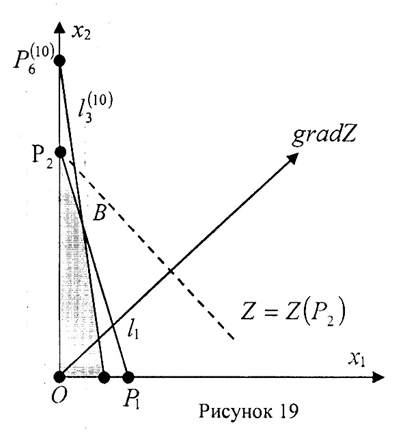

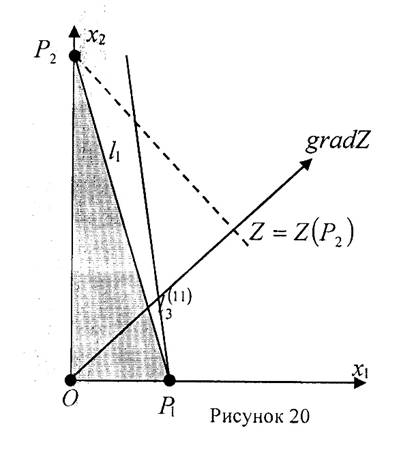
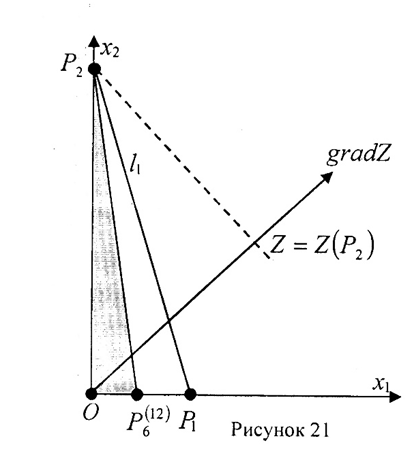
Переходим к решению двойственной задачи. Проверим условия «дополняющей нежёсткости».
Так как у*₂ > 0, значит u*₂= 0. Так как х*₁=0,то v*₁≥ 0, х*₂=222>0,то v*₂= 0. Получаем условия в двойственной задаче для оптимального плана: 3u₁*+ 7u₃*≥201; u₁*+u₃*=187. u*₂=0, Из уравнения выражаем u₁*:u₁*=187–u₃*. Подставляем это выражение в неравенство: 3·(187-u₃*)+7u₃*=561+4u₃*≥ 201 4u₃*+360≥0. Это условие выполняется при любых u₃*≥0. Положим u₃*=187t, тогда, 0 ≤t≤1. Выражаем через t оценку u₁*: u₁*=187(1–t).
Значение целевой функции в двойственной задаче: W_min=222∙187(1–t) +r₁∙0 +r₂∙187t. Так как r₂=222, то W_min=222∙187(1–t) +222∙187t= 222∙187 = 41514 руб.
Определим область D₇. Она должна удовлетворят условиям прямой задачи: y₁*=0, y*₂>0; y*₃=0, х*₁ =0, х*₂=222.

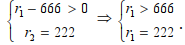D₁₀ определяется системой неравенств: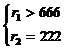

Построим область D₁₀ на плоскости О_r1r2 (рис.22).

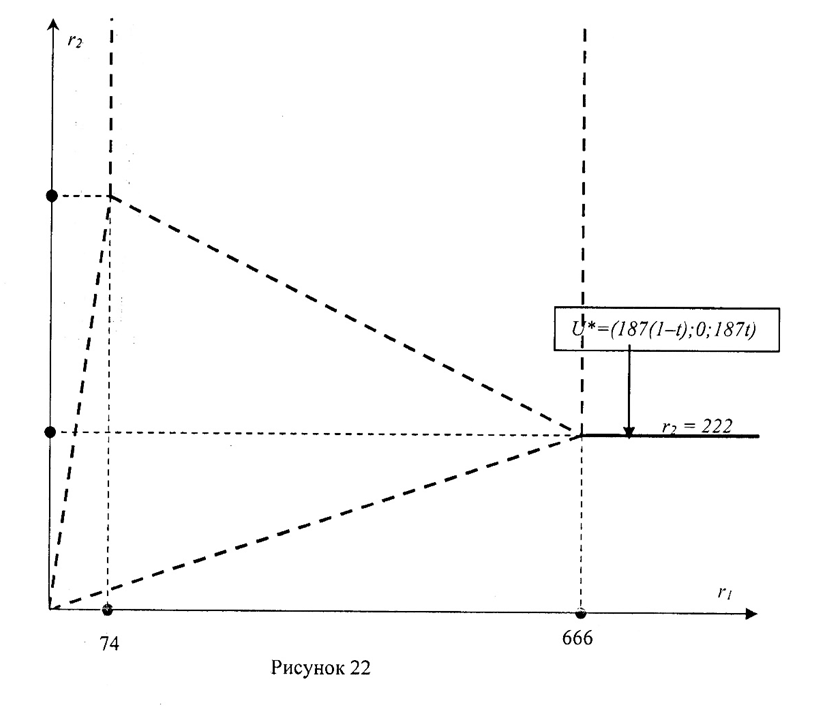
4.7. Избыточных ресурсов нет

Рассмотрим случай, когда все ресурсы будут дефицитные. Тогда y₁*=0, y₂*=0, y₃*=0.
Тогда оптимальное решение в прямо задаче будет удовлетворять системе условий.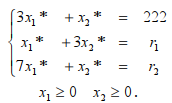
Возможные ОДР задач при этих условиях рассмотрены на рисунках 23, 25 и 27. Во всех этих задачах оптимальные планы разные. Поэтому каждую из задач мы рассмотрим отдельно.
1) На рисунке 23 представлено решение, когда объём выпуска продукции вида А больше нуля, а продукции вида В – равно нулю (х*₁ >0, х*₂=0). Оптимальный план – точка Р₁. Это точка пересечения прямо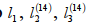и оси Ох1. Тогда 3х1*=222 и х1*=r1 и 7х1*=r2: Х*= (74;0).

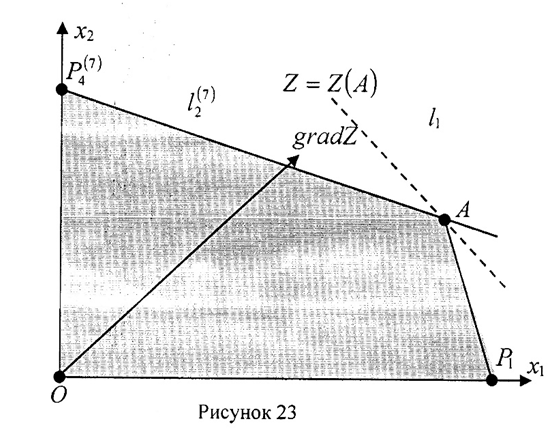
Из второго и третьего уравнений получаем значения для r₁ и r₂: r₁=74 и r₂=7∙74=518. Оптимальное значение целевой функции равно Z_max=201∙74 =14874 руб.

Решаем двойственную задачу:3u₁*+u₂*+7u₃*=201; u₁*+3u₂*+u₃* ≥187. Выражаем u2* через u₁* и u₃*: u₂*=201–3u₁*–7u₃*. Подставляем это выражение в неравенство: u₁*+3·(201–3u₁*–7u₃*)+u₃*=603–8u₁*–20u₃*≥ 187 8u₁*+20u₃*≤ 416 2u₁*+5u₃*≤ 104. Положим u₁*=52t, u₃*=20,8s, тогда 0≤t+s≤1. Тогда u₂*=201–3·52t–7∙20,8s u₂*=201–156t–145,6s. Вычислим v*₂: v*₂=52t +3·(201–156t – 145,6s )+20,8s–187=416–416 t–124,8s= 8∙(52–52t–15,6s), где 0 ≤t+s≤1. Найдём W_min: W_min=222·52t+74·(201–156t – 145,6s)+518 ·20,8s =3∙74·2,5∙20,8t+74·(201–3∙2,5∙20,8t – 7∙20,8s)+7∙74 ·20,8s =74∙201= 14874.
Определим область D₈. Она должна удовлетворят условиям прямой задачи: y₁*=0, y*₂=0; y*₃=0, х*₁ >0, х*₂=0.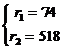. D11=A=(74;518).
Построим область D₁₁=A на плоскости О_r1r2 (рис.24).
2) На рисунке 25 представлено решение, когда объём продукции вида А равен нулю (х*₁=0), а объём продукции вида Б не равен нулю (х*₂>0).

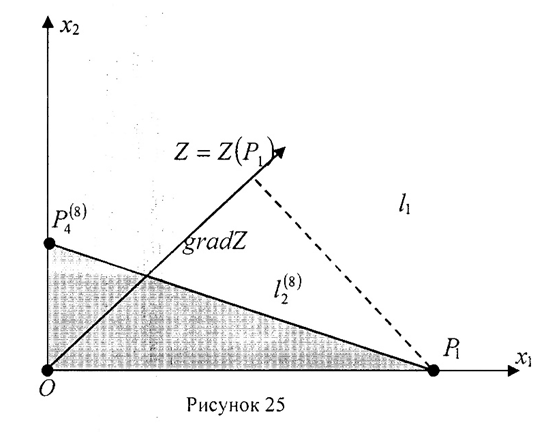
Оптимальный план – точка Р₂. Это точка пересечения прямой и оси Ох₂. Тогда х₂*=222, 3х₂*= r₁ и х₂*=r₂: Х*= (0;222). Значения r₁ и r₂: r₁=666, r₂=222. Оптимальное значение целевой функции равно Z_max=187∙222=41514руб.
Решаем двойственную задачу: 3u₁*+u₂*+ +7u₃*≥201; u₁*+3u₂*+ u3*=187. Выражаем u₁*: u₂*=187–3u₂*–u₃*. Подставляем это выражение в неравенство: 3·(187–3u₂*–u₃*)+u₂*+7u₃*=561–8u₂*+4u₃*≥ 201 8u₂*–4u₃*≤ 360 2u₂*–u₃*≤ 90. Положим u₂*=45t, u₃*=90s. Тогда u₁*=187–3·45t–90s u1*=187–135t–90s. Вычислим v*₁: v*₁=3·(187–135t–90s)+ 45t+7∙90s –201=3·(187–135t–90s)+ 45t+7∙90s –201=360 –360 t–360s=360∙(1–t–s). Так как v₁*≥0, то 0 ≤t+s≤1. Найдём W_min: W_min=222·(187–135t–90s)+r₁ ·45t +r₂∙90s. Так как r₁=666 и r₂=222, то W_min=41514–222·135t–222·90s+45t∙666 +90s∙222=41514–222·3∙45t+45t∙3∙222=41514.
Область D₁₂ представляет собой точку В=(666;222) (рис. 26).
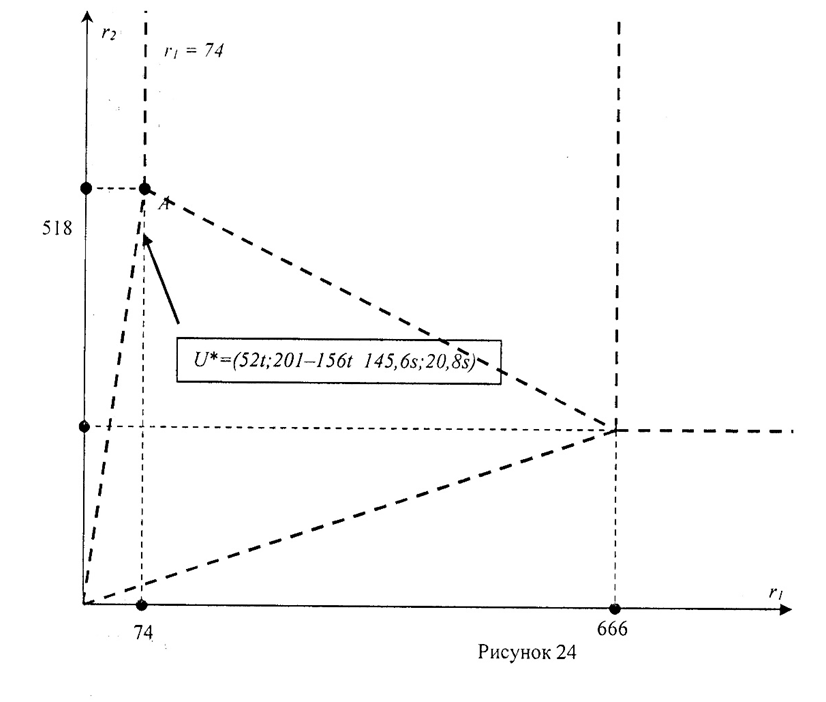
3) Рассмотрим случай, когда x*1>0, x*2>0 (рис. 27). В этом случае

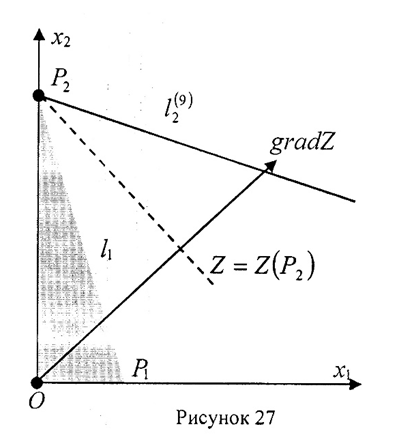
ОДР=OP₄⁽¹⁴)АР₅⁽¹⁴⁾. Оптимальной будет точка А, не лежащая ни на оси Ох₁, ни на оси Ох₂. Определяем координаты точки А, как точки пересечения трёх прямых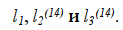Решаем систему уравнений:

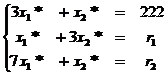. Решение системы:

Решаем двойственную задачу. Так как выполнятся условия y*₁=y*₂=y*₃=0, то все переменные в двойственной задаче могут принимать любые положительные значения. Так как x*₁>0, x*₂>0, то оба ограничения а двойственной задаче являются равенствами при оптимальном плане. Получаем:

.

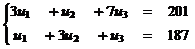Найдём решение этой системы преобразованиями расширенной матрицы.

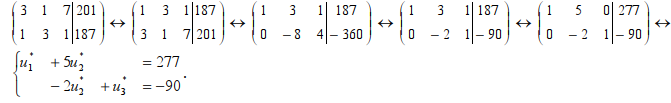
Так как все переменные в двойственной задачи положительные, то найдём границы изменения переменной u₂*. 277–5u₂*≥0, так как u₁*≥0; –90 +2u₃*≥0, так как u₃*≥0. Получаем, u₂*≤55,4 и u₂*≥45. Тогда 45≤u₂*≤55,4. Тогда u*₂ =45+10,4t, 0≤t≤1. Переменные u₁* и u₃* будут выражаться через t: u₁*=277–5·(45t+10,4)=225–225t=225(1–t), u₃*=2·(45+10,4t)–90=20,8t. Оптимальные планы в двойственной задаче определяются выражением: U*=(225(1–t); 45+10,4t; 20,8t), где 0≤t≤1.
Найдём значение W_min: W_min=222·52·(1–t)+r1·( 45+10,4t)+r₂· 20,8t=11544+45r1.
Область D₁₄ удовлетворяет условиям: 666 – r₁≥0, 3r₁–222≥0, r₁+2r₂=1110. Тогда D₁₄ определяется системой неравенств: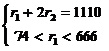. Решение для области D₁₄

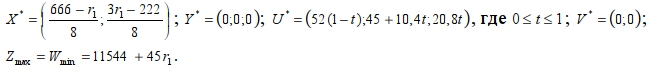
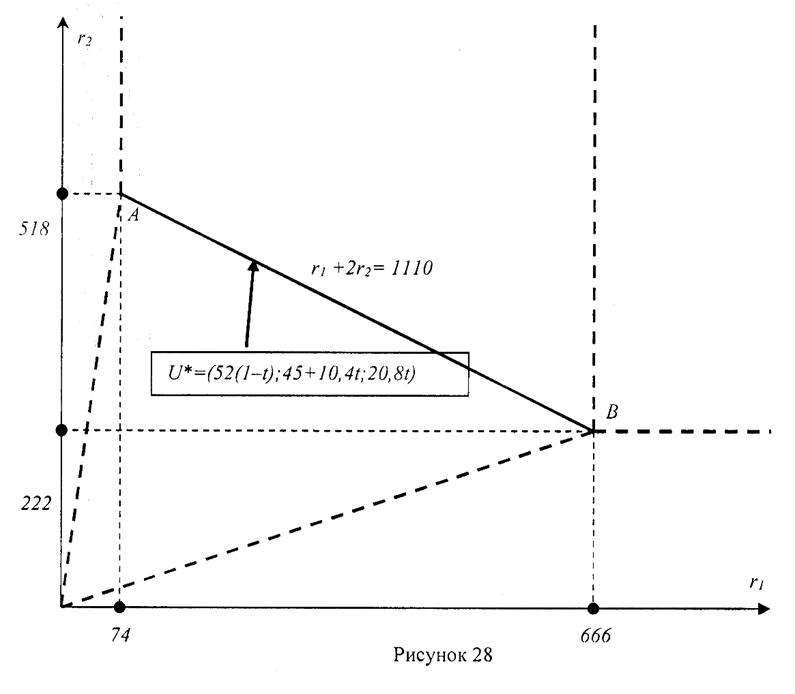
Построим область D₁₄ на плоскости О_r1r2 (рис.28).

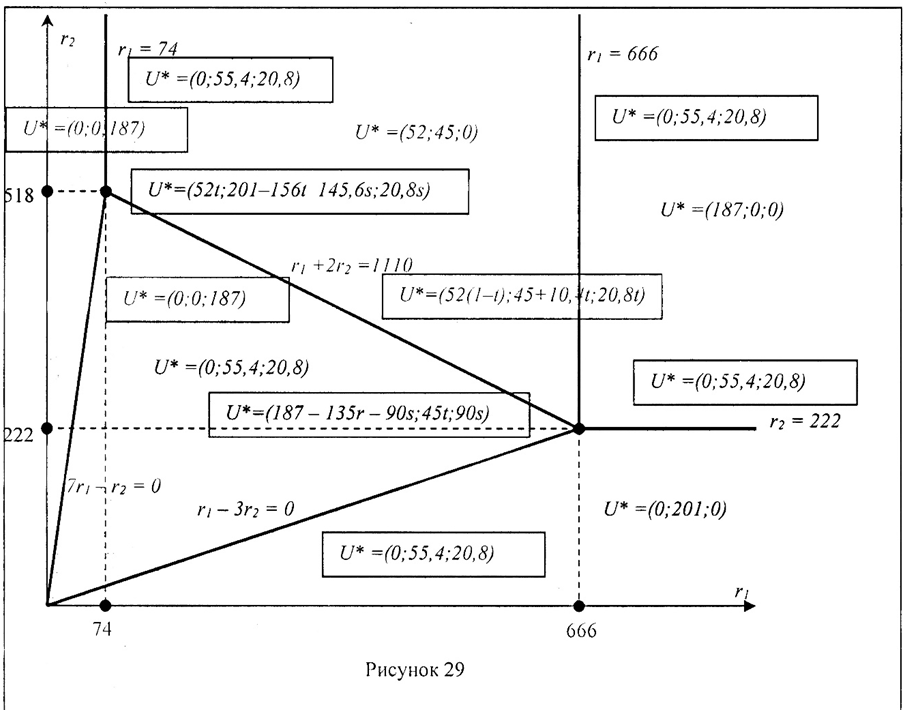
5. Карта предельных полезностей ресурсов

Мы рассмотрели все случаи для ресурсов. На основе этого строим карту предельных полезностей при изменении объёмов оборудования и трудовых ресурсов (рис. 29).

Карта предельных оборудования и трудовых ресурсов